二体の電子伝播関数の導出および応用

　現在コンピューターの進歩に伴い単分子のみならず、化学的に興味ある金属錯体や分子クラスターに対してもハートリー・フォック法を超える精度で量子化学計算を適用することが可能となってきました。しかし、未だ化学反応や光学応答に関して重要な知見をもたらす電子励起状態計算について、電子相関を含み系統的に発展可能な手法は、配置間相互作用(CI)法および結合クラスター展開(CC)法のみと言われています。
そこで我々は電子伝播関数法を用い、上記の主流とは異なったアプローチで一電子励起状態や二電子イオン化状態に対する知見を得る可能性を調べました。これから更なる伝播関数法の精度を向上させるためには、以下の展開が必要です。

参照系の展開。
伝播関数法は一般的なグリーン関数に基づくため、参照系の種類を選ばず、ハートリー・フォック参照系を素より、多配置参照系や密度汎関数(DFT)参照系においても展開可能です。
励起空間の拡張。
通常、一電子励起状態を計算するためには二電子励起や三電子励起空間を考慮し全空間を対角化する必要がありますが、伝播関数法では一電子励起空間に任意のn電子励起空間を繰り込むことで、全空間を対角化せずに高精度な励起エネルギーの計算が可能となります。
高次の摂動補正の導入。
各空間に対し摂動法による補正項を導入することで、高次の電子励起空間を繰り込むことと同様な効果が得られます。従って、たとえ二電子励起空間のみを主空間に繰り込んだとしても、主空間に二次の摂動補正を加えることで三電子励起空間の寄与の一部が考慮されます。

以上の展開により、我々はより高精度な電子励起状態計算方法の確立を目的とし研究を行っています。主な研究例として二電子伝播関数法によるオージェ電子スペクトルシミュレーションがあります。

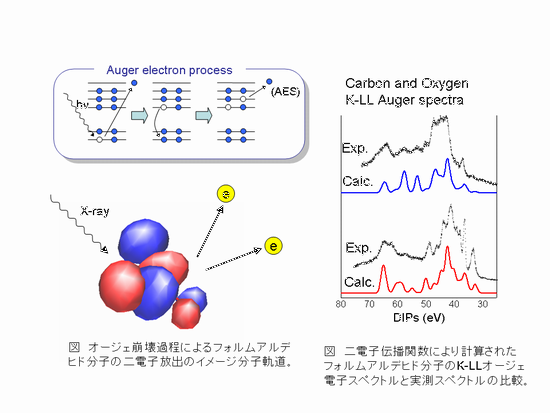
オージェ電子崩壊過程とスペクトルシミュレーション結果